Skip to main content

1.2 波函數和量子態

我們將深入探討波函數的概念、它在量子力學中的核心地位，以及如何用波函數來描述量子態。 這一章節將介紹波函數的數學形式、其物理含義，以及它如何被用來預測微觀粒子行為的概率。 此外，我們還將探討量子態的多種可能性，以及它們如何通過測量而決定。

波函數的基礎​

波函數的定義​

波函數，在量子力學中，是一種基本工具，用於描述一個量子系統的狀態。 這個概念的數學形式化是由薛定谔方程式所引導。 具體來說，對於一個單粒子系統，波函數是一個複數值函數ψ(x,t)\psi(x, t)， 其中xx表示粒子在空間中的位置，而tt代表時間。 波函數的模方∣ψ(x,t)∣2|\psi(x, t)|^2提供了粒子在時間t位於位置x的概率密度。這意味著找到粒子在某個特定位置的概率，是由波函數在該點的值的平方決定的。

波函數不僅包含了粒子位置的概率資訊，它還可以被用來計算其他物理量的期望值。 這種對波函數的理解強調了量子力學與古典物理學的一個關鍵區別：量子系統的狀態不再由確定的軌跡來描述， 而是由一個概率分佈來定義。這也意味著在量子力學中，測量的結果本質上是不確定的， 只有在進行實際測量後，系統的狀態才會決定於特定的結果。

波函數的數學性質​

波函數的數學性質對理解量子力學至關重要。首先，波函數是一個複數函數，意味著它具有實部和虛部。波函數通常在希爾伯特空間中被表達和處理，這是一種滿足特定數學條件的函數空間。波函數的歸一化是其另一重要特性，確保所有可能找到粒子的位置的概率總和為1。此外，波函數的疊加原理允許多個波函數相加形成新的波函數，顯示了量子系統的狀態可以是多種可能狀態的疊加。

量子態​

量子態的概念​

量子態是量子力學中一個核心概念，用以描述微觀粒子如電子、光子的物理狀態。在量子力學的框架內，量子態不僅關聯到粒子的位置、動量等傳統物理量，也包括量子特性如自旋和糾纏。量子態通常用波函數表示，這個波函數的絕對值平方給出了找到粒子在某個特定位置的概率密度。

與古典物理不同，量子態具有一個非常特殊的性質——疊加原理（superposition）。這意味著一個量子系統可以同時處於多個狀態的「疊加」中，直到進行測量時才確定為某一特定狀態。這種疊加狀態是量子力學的一個顯著特點，它允許系統展現出比古典物理更為豐富的行為模式。

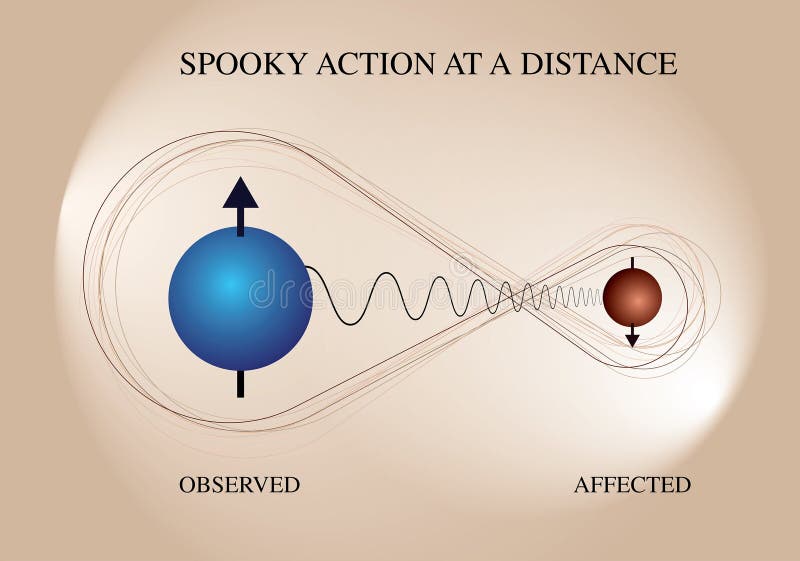
量子態的另一個關鍵概念是量子糾纏（entanglement）。當兩個或多個量子系統處於糾纏狀態時，它們的量子態無法單獨描述，只能作為一個整體來考慮。量子糾纏揭示了量子系統之間深層次的非局域性聯繫，即使它們相隔很遠，系統間的一個局部測量也會立即影響到整個糾纏系統的狀態。

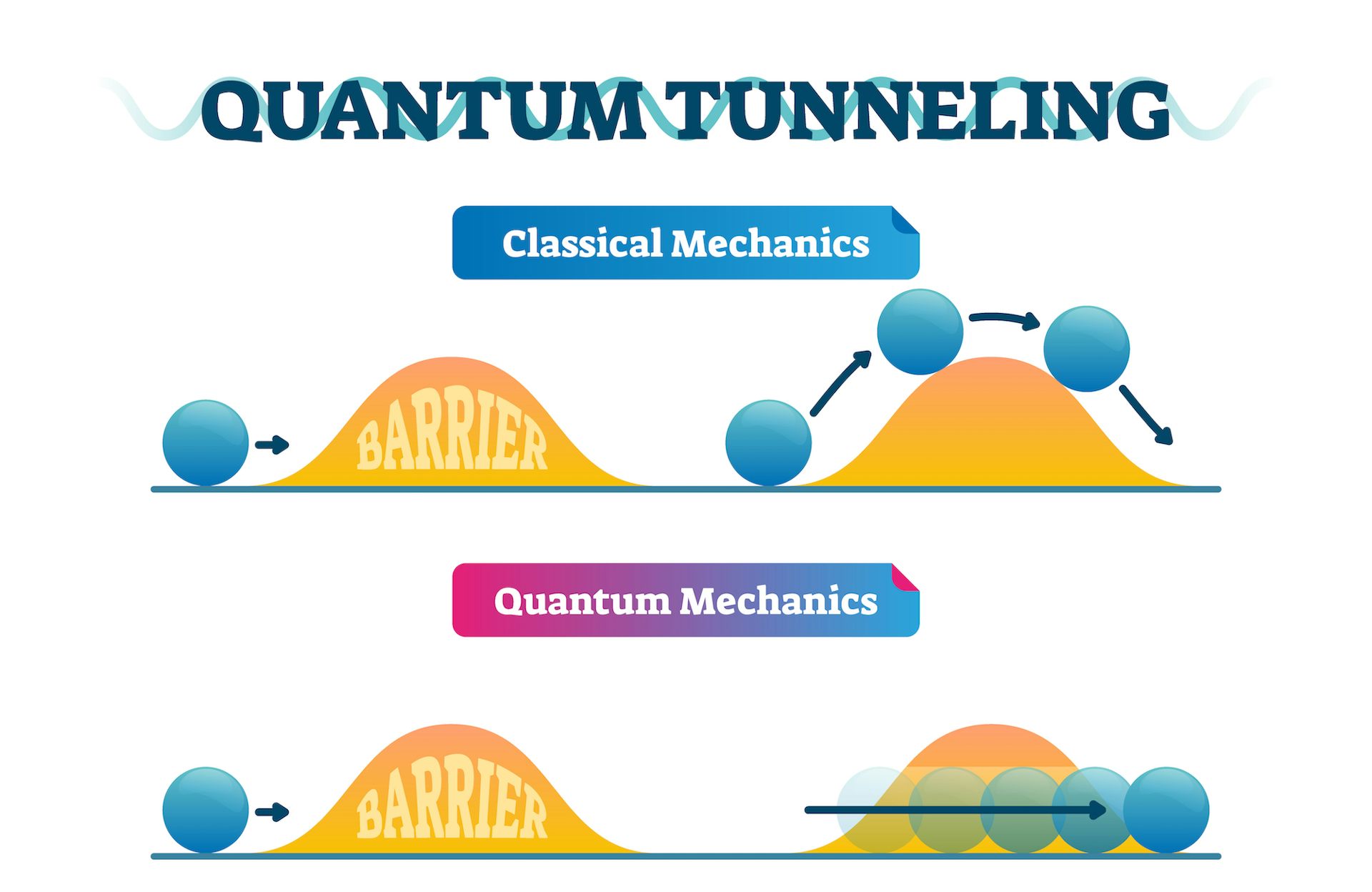
│量子還有一個很有趣的特性叫做量子穿越（Quantum Tunneling），一個量子會在一道牆的左邊，瞬間穿越到一道牆的右邊。 這個特性與我們巨觀的世界有很大的不同。我們的生活中，我往一面牆一直走過去，最後勢必會撞上那面牆。 但是在量子的世界就不是這樣，一個量子往一面barrier走過去，如果barrier很薄的話，這個量子是有機會出現在barrier的另外一側。 QT

狀態疊加與量子糾纏​

量子態的疊加原理是量子力學的一個基石。 根據這一原理，如果一個系統可以處於多個不同的態（例如∣ψ1⟩\ket{\psi_1}和∣ψ2⟩\ket{\psi_2}），那麼它同時也可以處於這些態的任意線性組合（疊加態）中。數學上，這可以表示為：

∣Ψ⟩=c1∣ψ1⟩+c2∣ψ2⟩\ket{\Psi} = c_1\ket{\psi_1}+c_2\ket{\psi_2}

其中，c1c_1和c2c_2是概率振幅，它們滿足∣c1∣2+∣c2∣2=1|c_1|^2+|c_2|^2 = 1。

量子糾纏是量子力學中一種非經典的相關性。 當兩個粒子系統處於糾纏態時，對其中一個粒子的測量立即確定了另一個粒子的狀態，無論它們之間的距離有多遠。 舉例來說，假設兩個粒子的糾纏態可以用下列形式表示：

∣Φ⟩=12(∣↑⟩A∣↓⟩B−∣↓⟩A∣↑⟩B)\ket{\Phi} = \frac{1}{\sqrt{2}}(\ket{\uparrow}_A\ket{\downarrow}_B - \ket{\downarrow}_A\ket{\uparrow}_B)

這裡，∣↑⟩\ket{\uparrow}和∣↓⟩\ket{\downarrow}分別代表粒子的兩種不同自旋狀態，下標 A 和 B 分別表示兩個不同的粒子。 這個表達式顯示了無論測量 A 或 B，其結果都會立即影響到另一個粒子的狀態。

量子態的測量與坍塌​

量子態的測量是量子力學中的一個關鍵過程，它涉及對量子系統狀態的觀察與檢測。 根據量子理論，當對一個處於多種可能態的疊加中的量子系統進行測量時，系統會「坍塌」到其中一個特定的狀態。 這一過程稱為「波函數坍塌」，是量子測量的一個核心特徵。

在這一過程中，波函數的疊加態會因測量而瞬間轉變為某個特定態。 例如，對一個處於「上」和「下」自旋疊加狀態的電子進行測量，結果將隨機地得到「上」或「下」的一個特定自旋狀態。 這個測量結果的隨機性是量子力學的一個基本特性，與經典物理中的確定性顯著不同。

此外，量子測量的非確定性還涉及到量子系統的糾纏特性。 當兩個量子粒子處於糾纏狀態時，對其中一個粒子的測量會即時影響到另一個粒子的狀態，無論它們相隔多遠。 這反映了量子系統的非局域性，也是量子力學中最令人著迷的現象之一。

量子態的測量與坍塌是理解量子系統如何與周圍世界交互的關鍵，也是許多量子技術，包括量子計算和量子通訊的基礎。

波函數的演化​

薛定谔方程​

時間演化與動力學​

量子系統的穩定性和過渡​

波函數與概率解釋​

概率密度的計算​

統計解釋與物理意義​

波函數解釋的哲學問題​

實驗中的波函數​

雙縫實驗與波函數​

量子力學實驗驗證​

現代量子實驗技術​